手写AI算法之KMeans聚类算法

K-means 是最常用的基于欧式距离的 机器学习 聚类算法，其认为两个目标的距离越近，相似度越大。K-means是无监督学习的基础算法。

一、牧师—村民模型

四个牧师，随机选了四个布道点，村民到离自己最近的布道点听课。

每个牧师统计自己的课上村民的地址，把布道点搬到中心位置。

就这样，牧师每个礼拜更新自己的位置，村民根据自己的情况选择布道点，最终稳定了下来。

二、K-means 的算法步骤

1、选择初始化的 n 个样本，作为初始聚类中心 a=a1,a2,a3...an；

2、针对数据集中每个样本 xi，计算它到 k 个聚类中心的距离，并将其分到距离最小的聚类中心所对应的类中；

3、针对每个类别 aj ，重新计算它的聚类中心（即属于该类的所有样本的质心）；

4、重复上面 2 3 两步操作，直到达到某个中止条件（迭代次数、最小误差变化等）。

三、优缺点

1、容易理解，算法复杂度低；

2、K值需要人为设定，不同K值对结果影响较大；

3、对初始的簇中心敏感，不同选取方式会得到不同结果；

4、对异常值敏感，不适合太离散的分类。

四、代码示例

1. 生成随机样本

from matplotlib import pyplot as plt
from sklearn.datasets._samples_generator import make_blobs

X, _ = make_blobs(200, 2, centers=[[2, 3], [6, 8]])
plt.scatter(X[:, 0], X[:, 1])
plt.show()

2. 定义类，并初始化

class KMeans():
   def init(self, k, iter_max):
       self.k = k #聚类数量
       self.iter_max = iter_max #最大迭代次数

   def fit(self, X):
       self.X = X #样本数据

3. 随机生成中心点

# 随机中心点
idxs = random.sample(range(len(self.X)), self.k)
self.centers = self.X[idxs]

4. 分类和计算距离

def _classify(self):
    sum_dist = 0
    self.classes = [[] for i in range(self.k)]
    self.labels = []
    for x in X:
        dists = ((np.tile(x, (self.k, 1)) - self.centers)**2).sum(1)
        #找最小距离
        label = np.argsort(dists)[0]
        self.labels.append(label)
        #累加最小距离
        sum_dist += dists[label]
        #分类
        self.classes[label].append(x)
    #判断是否收敛
    if abs(self.sum_dist - sum_dist) >= 0.1 and self.iter_num<=self.iter_max:
        self.sum_dist = sum_dist
    else:
        return True

5.  更新中心点

def _up_centers(self):
    centers = []
    for lst in self.classes.values():
        arr = np.array(lst)
        centers.append(arr.mean(axis=0))
    self.centers = np.array(centers)

6. 循环迭代

while True:
    #分类及最小距离
    r = self._classify()
    self.iter_num += 1
    if r:
        return self
    #更新中心点
    self._up_centers()

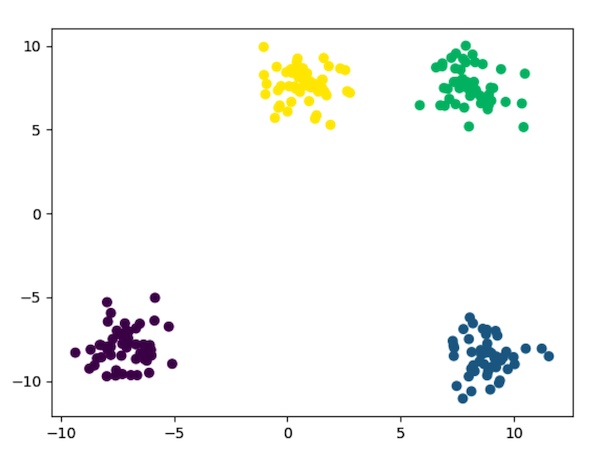
7. 效果可视化

colors = ['red', 'blue', 'green', 'yellow']
for x, l in zip(X, kmeans.labels):
    plt.scatter(x[0], x[1], c=colors[l])
plt.show()