动态规划之钢条切割问题

某公司出售钢条，出售价格与钢条长度之间的关系如下表：

问题：现有一段长度为n的钢条，求切割钢条方案，使得总收益最大。

分析

长度为4的钢条，所有切割方案如下：

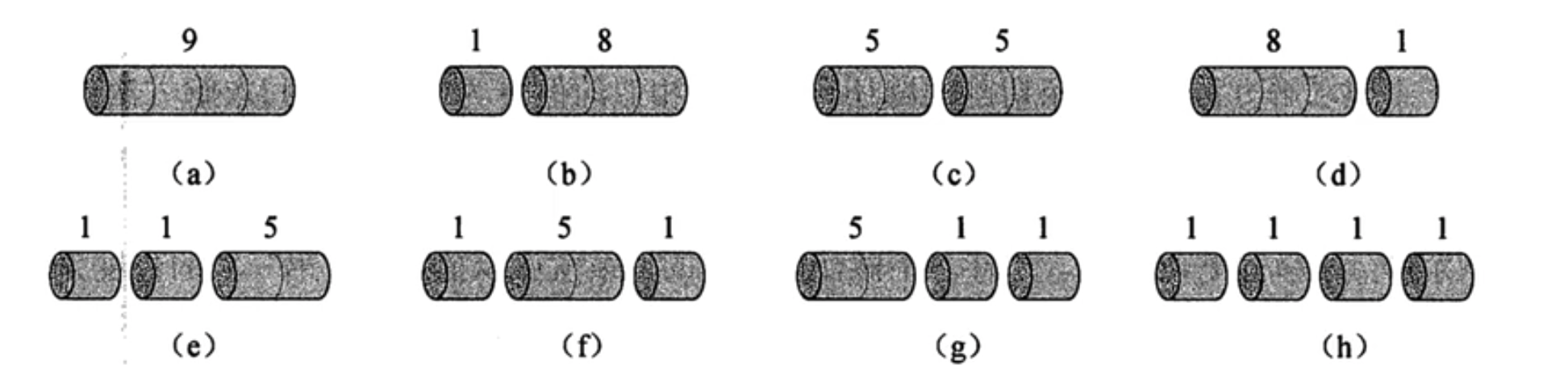
思考：长度为n的钢条的切割方案有几种？

答案：2^(n-1)种，总共有n-1个切割位置，可以选择切或者不切。

递推式

设长度为n的钢条，切割后的收益指为r(n)，可以得到递推式：

r(n) = max(p(n), r(1)+r(n-1), r(2)+r(n-2)...,r(n-1)+r(1))

1) 第一个参数p(n)表示不切割

2) 其他n-1个参数，表示将钢条切割成i和n-i两段

3) 切割后的i和n-i段又可以继续切割，但这两段的最大收益前面已经得到

4) 考察所有i，选择其中受益最大的方案即可

问题的本质是，将全局最优问题，转化成了两个最优子结构加和的问题。

代码示例

def cut(plist, n):
    rlist = [0]  # 最大收益
    clist = [[]]  # 最大收益对应切割方案
    for i in range(1, n+1):
        r = plist[i]  # 不切割
        c = [i]  # 不切割对应方案
        for j in range(1, i):
            # 切割成 j 和 i-j 两段
            new_r = rlist[j] + rlist[i-j]
            if r < new_r:  # 有更优方案更新
                r = new_r
                c = clist[j] + clist[i-j]
        rlist.append(r)
        clist.append(c)
    return rlist[-1], clist[-1]

plist = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]

print(cut(plist, 9))